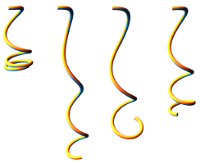Distribution of software

Dual licensing policy

We provide a few samples of source codes accompanying some of our main publications. Most of our source codes are distributed according to a dual licensing policy:

a GNU GPL licence, freely available and mainly targeted for academic researchers. Sharing software resources to the research community indeed helps researchers conduct reliable benchmarking work, and is also a way to mutualize efforts so as to build up better methods and systems. If you sign up for a GPL license and modify or improve the code, we encourage you to distribute your changes to the community. Note that according to the GPL licence, you are not allowed to distribute a software based on the original code source or on any modified version of it, without distributing the corresponding sources.
a commercial proprietary licence, mainly targeted for people working in industry, and for anybody who would like to have a different usage from the one that is required by the GPL licence. If you are working for a private company, as long as you respect the terms of the GPL and in particular do not need to sell nor distribute your software (depending on our code) without distributing the source code, you may well use the free GPL license. Otherwise you have to acquire a proprietary license. Furthermore, while this is not requested by the GPL license, we strongly encourage you to acquire a commercial license if you plan a long-term project using our code, even if this is for internal usage only and not to be integrated into a commercial software. This way you will contribute to the research cost which, in our case, is mostly funded by public resources. To get a commercial license, please e-mail us (Florence (dot) Descoubes (at) inria.fr).

If you are using our source code for building some new public material such as a research publication, a GPL source code, or results such as images or movies, please cite our work (by citing the paper which is related to the distributed software).

Of course, although we do not commit ourselves to maintain the code, we are happy to be informed about where and how our work is being used. So please feel free to contact us and provide us with feedback !

Source codes available for download (under the GNU General Public License if not mentioned otherwise)

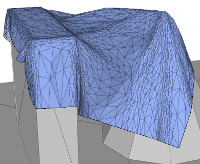
	Argus-distribution, simulating adaptive cloth dynamics with (nonsmooth) frictional contact. This code is the reference implementation of our adaptive cloth frictional contact paper. Citation: Jie Li, Gilles Daviet, Rahul Narain, Florence Bertails-Descoubes, Matthew Overby, George Brown, and Laurence Boissieux. An Implicit Frictional Contact Solver for Adaptive Cloth Simulation, ACM SIGGRAPH 2018. License: The Argus-distribution code acts as an open-source module which calls two external open-source libraries, So-bogus and (a modified version of) ARCSim. The two latter libraries use different open-source licenses, please refer to the Argus-distribution LICENSE file for details).
	Sand6, simulating granular material as a continuum medium with (nonsmooth) Drücker-Prager rheology. This code is the reference implementation of our semi-implicit MPM granular simulation paper. Citation: Gilles Daviet and Florence Bertails-Descoubes, A Semi-Implicit Material Point Method for the Continuum Simulation of Granular Materials, ACM SIGGRAPH 2016.
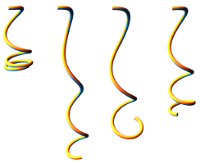
	Cloc, simulating the dynamics of arbitrary curly thin elastic rods. This code is the reference implementation of our Super Space Clothoids paper. Citation: Romain Casati and Florence Bertails-Descoubes, Super Space Clothoids, ACM SIGGRAPH 2013.
	Approche, converting a space curve into a smooth piecewise helix. This code is the reference implementation of our 3D Floating Tangents paper. Citation: Alexandre Derouet-Jourdan, Florence Bertails-Descoubes, and Joëlle Thollot, Floating Tangents for Approximating Spatial Curves with \(G^1\) Piecewise Helices, Computer-Aided Geometric Design 2013. Note: We have also been leveraging this code in our Inverse Dynamic Hair Modeling paper to convert splines into the geometry of super-helices.
	So-Bogus, a fast and robust solver for capturing frictional contact between many Lagrangian systems with exact Coulomb friction. This code is a new reimplementation by Gilles Daviet and serves as a reference code for our Hybrid Iterative Solver paper. The method significantly improves robustness and scaling up compared to Double Loop. Citation: Gilles Daviet, Florence Bertails-Descoubes, and Laurence Boissieux, A Hybrid Iterative Solver for Robustly Capturing Coulomb Friction in Hair Dynamics, ACM SIGGRAPH Asia 2011. Note: We have also been leveraging this code in our Super Space Clothoids paper to simulate dry frictional contact, and in our Inverse Dynamic Hair Modeling paper to efficiently solve the inverse problem formulated as a large convex second-order cone quadratic program (particular case of the nonconvex frictional contact problem).
	Double Loop, a simple Newton solver based on the Alart-Curnier formulation to capture frictional contact between a few Lagrangian systems with exact Coulomb friction. This code is the reference implementation of our Nonsmooth Newton Solver for Fiber Assemblies paper. Citations: Florence Bertails-Descoubes, Florent Cadoux, Gilles Daviet, and Vincent Acary, A Nonsmooth Newton Solver for Capturing Exact Coulomb Friction in Fiber Assemblies, ACM Transactions on Graphics 2011. Pierre Alart and Alain Curnier, A mixed formulation for frictional contact problems prone to newton like solution methods, Computer Methods in Applied Engineering and Mechanics 1991. Note: This code is easy to use and a full example with a colliding sphere is provided. However, be aware that since then we have been much improving the robustness of this solver by designing the Hybrid Iterative Solver where a recent implementation is given by So-Bogus.

Authors

So far, people that have been involved in the design and development of the distributed codes include Florent Cadoux, Romain Casati, Gilles Daviet, Alexandre Derouet-Jourdan, Jie Li, Rahul Narain, Matthew Overby, George Brown, and Florence Bertails-Descoubes.

Back to the main page.